Bubble Decompression
Strategies

PART I: BACKGROUND and THEORY

Copyright 1995 by Eric Maiken

 

 

This article was published in a different form in DeepTech, Issue 6. It summarizes about one-third of my Bubble Decompression Strategies presentation at the tek95 conference.

Beer      Balloons

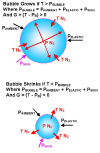
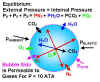
Introduction

Unlike abstract frontiers of knowledge, the boundary between the known and unknown is clearly visible underwater--often beginning near 130 ft (40 m). In addition to exploring this edge, technical divers also extrapolate beyond the known with their decompression practice. Examples include the use of exotic ascent gasses (such as argox and neox) and the advent of modern rebreathers with their attendant possibilities for gas mixtures and duration at depth. In the face of change, it is important to pause and critically examine decompression methods before conducting hyperbaric experiments on yourself. This article is the first of two concerning how the presence of bubbles in a diver's tissues affects decompression. After covering the theoretical basis for bubble decompression models in this first article, we will go on to see how bubble ideas can be incorporated into real-world decompression scenarios in part II.

Most civilian decompression meters, software, and tables are derivatives of neo-Haldane calculation methods, often modeled after Buhlmann's work. Ascents are controlled by limiting tissue supersaturation in a set of gas-loaded compartments (hypothetical tissues). In the laboratory, a current focus in decompression modeling involves formulating ascent schedules that report the statistical confidence in a certain probability of decompression illness (DCI). For example, a schedule might state that you can be 95% sure that the profile will have a bends incidence of 2%. Statistical models form reliable predictions within the "known." However, without a fundamental model, statistics cannot be used to extrapolate to untested regions (new combinations of depths and bottom times, gas mixtures and switches, etc). This is both a strength and a weakness, for only by grounding tables in experimental data can a meaningful definition of what is "known" be made. Yet, senior researchers insist that they are not confident that they even have a handle on air diving--let alone the use of multiple inert gases. It will be a long time before decompression calculation methods of universal validity become available. A fundamental, first-principles model may never be developed. Meanwhile, divers will go deeper for longer durations, using whatever map of the territory is available.

Any diver who has been routinely monitored with a Doppler meter can tell of times they bubbled--even after following a conservative ascent schedule. As unnerving as the experience is, the first thing that you wonder after hearing low-grade bubbles is "why don't I feel bent?" The answer may be that the body has the ability to handle small amounts of bubbles without undue stress. There is substantial evidence that the body's tissues contain cavities and bubble nuclei before making a dive. These preexisting voids are activated into growth with the application and reduction of pressure associated with diving. Bubbles are especially prone to growth when surrounding tissue is heavily loaded with dissolved gas, such as might be expected following long, deep or repetitive dives.

It is possible to adopt decompression strategies to minimize the formation and growth of bubbles. While this might be the objective of all decompression schedules, the surprising result is that bubble elimination strategies are often contrary to the recommendations of traditional diving tables and therefore seem counter-intuitive. For instance, decompression stops called for by bubble models are much deeper (often within a few ata of bottom) than corresponding neo-Haldane tables. We will see why this is so when we consider the physics of bubbles and look into the details of some bubble models.

 

A Short History of the Bubble Models

The idea that divers could develop bubbles, yet not display overt symptoms of the bends is nearly as old as the sport. Behnke, in the early 1950s, termed these asymptomatic cases silent bubbles. A decade later, Brian Hills of Australia introduced a method for minimizing the formation and growth of bubbles by advancing the "thermodynamic" calculation of decompression tables, culminating in the publication of the classic book Decompression Sickness (Ref. 1) in 1977. Therein, he gave clear discussions of concepts such as the inherent unsaturation of tissue (oxygen window) in addition to detailing his method for decompressing divers at zero supersaturation. Hills' tables stipulated initial stops far deeper than the US Navy (USN) profiles. Hills believed that the USN's tables encouraged formation of bubbles via a long ascent to a relatively shallow first stop and that the long ten-foot stop served as therapy to reduce bubbles formed by the extreme first pull upward.

Though Hills' ideas for decompression methods were firmly based in experiment, experience and theory, the resulting unconventional ascent schedules met with derision. The introduction of Doppler monitoring techniques in the late 1960s substantiated Hills' belief that divers were in fact bubbling on the USN tables. Although hopes that Doppler might be used as real-time feedback for decompression haven't materialized, the idea still holds that the prevention of bubbles will minimize risk of DCI.

Following Hills, researchers at the University of Hawaii postulated that a common basis of all DCI might be that the insult initiated in aqueous tissues that comprise the bulk of living creatures. They conducted a series of experiments that resulted in formulation of the Varying Permeability Model (VPM) (Ref. 2). As in Hills' model, VPM tables call for deep first stops to keep gas in solution so that it can be eliminated through the circulation rather than flow into bubbles. Wienke extended the VPM to include repetitive and multi-day diving in the Reduced Gradient Bubble Model (RGBM) (Ref. 3). A major equipment manufacturer slated the RGBM for implementation in diving meters in the early 1990's, though a product was never released.

Currently, a number of modeling efforts incorporate bubble-mechanical principles into the calculation of decompression schedules. Models under development at Duke University, NASA, and commercial diving firms incorporate both bubble mechanics and statistical analysis of DCI data. Technical divers already employ decompression procedures consistent with bubble models ad-hoc in their planning (see Richard Pyle's prescription for deep stops Ref. 4 ). Yet, the justification of these methods is often given in terms of operational concerns and neo-Haldane viewpoints rather than bubble mechanics.

 

Physiological Issues

Divers are not passive systems like the inanimate gelatin used in laboratory models for developing the VPM. The ability of the body to react to stimuli and stresses hinders deterministic decompression models. The physiological complexities of this feedback cycle are daunting. For instance, the biochemical reactions to the presence of gas bubbles can compound problems facing a DCI victim by initiating clotting and complement activation. The bubbles themselves can form obstructions in arteries, with severe consequences to the nervous system. On a less urgent level, even high partial pressures of oxygen can trigger responses such as the reduction of blood perfusion. The reduced flow to tissues diminishes out-gassing to the circulatory system, resulting in larger tissue tensions, encouraging bubble growth.

A comprehensive approach to building effective decompression tables requires input from a wide range of specialties. Even if we step back from the goal of building a universal model, it is still possible to make recommendations for decompression procedures that are consistent with minimizing the occurrence and growth of bubbles. This is where the fundamental perspective of physics can provide guidance for avoiding bubble formation and growth. Most importantly, mechanistic recommendations must be weighed against physiological, medical, and operational concerns.

During decompression, there are competing pathways for the flow of gas that has been absorbed by tissues while diving (Fig. 1). The challenge to table designers (and ultimately decompressing divers) is to keep tissue gas in solution while ascending so it can be eliminated by diffusion to the circulation. Assumptions inherent in neo-Haldane decompression models are inappropriate if gas has formed free phases in a diver's body. At best, decompression schedules that ignore free phases lead to bubble growth and ineffective gas elimination. For example, consider that DCI victims (who are likely bubbling) are compressed to relieve their symptoms. From this painfully practical example, we see that if a diver bubbles, the quickest way out of the water is to stay deep (pressurized), rather than pull stops as close to the surface as possible as standard decompression methods encourage.

Click to enlargeFig. 1. Dissolved gas can diffuse from the tissue into either the circulation or bubbles. Dissolved gas in circulation is easily eliminated in the lungs. Free gas in bubbles presents problems by greatly increasing out gassing time

BUBBLE PHYSICS

A glass of your favorite carbonated beverage will come in handy for this section. An intuitive understanding of how bubbles work can be gained from observing a glass of cola, champagne or beer.  Other models provide further insights that guide us in designing procedures for keeping bubbles as small as possible.

A bubble has an internal pressure that is generally different from the tension of inert gas in surrounding tissue. A bubble's size is key to determining whether it will shrink or grow. Bubble size is closely linked to its internal pressure through effects such as skin tension, the elasticity of surrounding tissue, and Boyle's law. The most important factor in minimizing bubble growth is keeping internal bubble partial pressures greater than (or equal to) tissue tensions. This is accomplished by setting stages deep and astutely choosing breathing gases. A common approach in bubble models is to limit the volume of gas freed from solution during ascent rather than set tissue tensions limits (as M values do in neo-Haldane calculations). The conditions under which bubbles grow or shrink (Fig. 2) can be studied by considering what factors affect changes in bubble size (Fig. 3).

The mathematical description of how each gas flows between tissue and bubble is given by a diffusion equation, which is distinct from the simple rate equations that yield exponential in/out gassing. A conceptual diffusion equation is easy to solve (Fig. 4). All we need do is account for those factors that make bubbles grow and those that make them shrink. Reality is a bit more complicated because multiple gasses can diffuse independently, causing a coupling of equations. For each inert gas:

Click to enlargeFig. 2. The pressure of gas dissolved in tissues is termed tension. The sum of the partial pressures of the free gases inside a bubble adds up to the total internal pressure of the bubble. The Bubbles will grow or shrink, depending on whether the gases in the surrounding tissue sum to a tension T that is greater or smaller than the bubble's internal pressure PBUBBLE. In either case, a pressure gradient G = (T - PB) across the skin of the bubble drives the flow of gas.

When G is positive, tissue tension is greater than bubble pressure, leading to bubble growth by inward flow of gas. G is negative if tissue tension is less than bubble pressure, leading to bubble shrinkage by outward flow. The objective of bubble models is to keep G negative (or zero) by appropriately setting ascent stage depths and choosing gas mixtures to encourage bubble out gassing to tissues. The deep stops of the bubble models keep PAMBIENT large, which in turn keeps PBUBBLE large and G negative to force out gas. By choosing ascent gases that "open the oxygen window" as wide as possible and as early in the ascent as possible, tissue tension is reduced, helping to keep G negative. The VPM and RGBM treat tissue tensions just like the neo-Haldane models. The rate of In gassing and out gassing of dissolved gas is modeled as an exponential rate equation.

Click to enlargeFig. 3. A bubble will remain stable in size if pressure balances in and outside. In equilibrium, the sum of the external hydrostatic mechanical pressures pressing inward will balance the summed partial pressures of the free gases within the bubble pressing outward. In this figure, the mechanical pressures are due to tissue elasticity, the bubble's skin tension, and the ambient pressure, which is proportional to depth. A nitrox diver's bubbles could contain nitrogen, carbon dioxide, water vapor, and possibly oxygen. All these gases will diffuse in or out of the bubble independently to balance internal free-gas partial pressures with the external partial tensions of gas dissolved in tissue. The bubble will grow or shrink depending if gas is coming or going.

The Varying Permeability Model was named for the skin of surfactant molecules postulated to surround bubbles. The skin is thought to be permeable to gases for low pressures and impermeable to gas at high pressures.

The time rate of change of a bubble radius is proportional to:

A: The surface area of the bubble. As with opening a window wider in a breeze, the greater the open area A, the more flow is possible.

D: The diffusivity of gas in surrounding tissue. This is a measure of how fast gas flows to equalize pressure differences. Diffusivity is accounted for phenomenologically in Neo-Haldane Trimix calculations by scaling tissue half-times as the inverse ratio of the square root of gas masses. That is, He half-times are (1/2.7)xN2 half-times.

S:The solubility of gas in tissue. The more soluble the gas, the higher the concentration of gas that is available to be absorbed by the bubble from saturated tissue.

G: The gradient of partial pressure across the bubble surface. G = T - Pb, where T is tissue tension and Pb is the pressure inside the bubble. G is positive if partial tissue tension exceeds bubble partial pressure, causing bubble growth. G is negative if bubble pressure exceeds tissue tension causing bubble shrinkage. The magnitude of a negative G is essentially a measure of the oxygen window Ref. 5

The time rate of change of a bubble radius is inversely proportional to:

r : The density of diffusing gas.

V: The volume of the bubble. With the volume having the opposite effect of area A on growth, the net result is bubble growth ~ (A / V) = 1/radius.

Click to enlargeFig. 4. The two diagrams illustrate how a bubble responds to differences between its internal pressure (red) and the tension of gas dissolved in the surrounding tissue (green). 

The upper figure's green curve is just the standard exponential compartment out gassing modeled by many commercial decompression programs.

The lower picture represents a "visual" solution to the diffusion equation. While the tissue tension of gas is greater than the bubble, G is positive, leading to bubble growth. The bubble shrinks once the tissue has off-gassed sufficiently for the tension of the inert gas to fall below the bubble pressure.

Click to enlargeFig. 5. Optimal inert gas elimination depends on how much of the gas is dissolved in tissues or free in bubbles. This figure shows how nitrogen in a nitrox diver's tissues or bubbles can be eliminated according to two opposing strategies. Real decompression schedules should balance these extremes.

Neo-Haldane models assume that all of the gas is dissolved and that the pressure gradient between the tension of gases dissolved in tissues and in the arteries drives elimination. The dissolved gas elimination gradient is maximized by reducing the arterial tension to the lowest possible value. This is accomplished by either ascending to reduce the depth D or by reducing the nitrogen fraction fN2 of the breathing mix. The ascent depth ceiling is limited by the "M values," or a and b coefficients in the case of the Bhulmann/Keller model.

Bubble models try to limit the total volume of gas that is allowed to form bubbles. This volume is controlled by keeping stops deep enough to keep the internal pressure of enough bubbles higher than the gas tension in surrounding tissues. Tissue tension is simultaneously minimized by selecting low fN2 breathing mix and ascending as much as possible to keep the volume of free gas below the critical volume.

 

The driving force eliminating free phases is opposite from dissolved gas. It is the oxygen window rather than the tissue tension T that controls free phase elimination. To eliminate bubbles, keep G negative by staying as deep as possible to force Pb to be larger than T. Think: G = growth--and negative growth is shrinkage. 

The quickest route out of the water from a neo-Haldane viewpoint is to minimize your depth (within the limits set by M values). An extreme version of this would be to ascend on a dive computer's ceiling alarm rather than at conventional 10-foot increments. From this viewpoint, a minimum depth causes maximum elimination gradient between gas dissolved in tissues and arterial gas tension. That is, if dissolved N2 tension T decreases at a rate proportional to the difference between arterial tension ppN2 = fN2 x (1 + D/33) and T, then off-gassing will increase as (ppN2 - T) becomes more negative. This occurs as a diver ascends because D, and hence, ppN2 decrease (upper Fig. 5).

In the case of bubbles, the opposite holds. The most efficient elimination of free phases occurs at maximal depth (lower Fig. 5). The rate of bubble collapse is proportional to G, the gradient between tissue tension and bubble internal pressure: (T - Pb). With bubble internal pressures increasing with ambient pressure (Pb = PAMBIENT + PSKIN + PELASTIC), a negative G occurs if Pb exceeds T. So we go deep to shrink bubbles.

Reality is in between the two extremes (what goes down must come up). The optimal strategy for inert gas elimination should effectively eliminate both free and dissolved gas. With this aim, it is best to stay at high ppO2 (within CNS toxicity limits) to encourage elimination of dissolved gas. By simultaneously keeping external pressure maximized, the O2 window is open to its fullest. The conventional 10-foot stop might well be eliminated altogether in meeting this goal.

We are now prepared to make some practical recommendations for decompression strategies based in bubble mechanics. This is where part II of this series will pick up the story. There, bubble ideas will be applied to the real water-world by considering practical recommendations that arise naturally from bubble models. Topics up for consideration include:

  • The best (though usually ignored) reason for pulling your 10-foot stop at twenty feet on oxygen.
  • How to open the oxygen window as wide and early as possible during ascents.
  • The strong physical argument in favor of in-water-recompression.
  • Inert gas counter-diffusion and why argon suit-inflation gas shouldn't cause problems.
  • Bubble amplification due to inappropriate gas switches at constant pressure.
  • Why rapid deep ascents are a bad idea for dives deeper than 9 ata.
  • Why diving deep enough, often enough can be good for you.

So there you have the background. A little more detail can be found in Ref. 6. Above all, I hope this article encourages critical discussion in the technical diving community regarding current decompression practice.

 

 

References

(1) B. Hills, Decompression Sickness. John Wiley & Sons, Ltd. (1977). Clear and compelling. Back to text .

(2) D.E. Yount, D.C. Hoffman, On the Use of a Bubble Formation Model to Calculate Diving Tables. Aviation, Space, and Environmental Medicine, February, 1986. To really understand the mechanics of the VPM, write a computer program using the algorithm in this paper. Back to text.

(3) B.R. Wienke, Basic Decompression Theory and Application. Best Publishing Co. (1991). Thorough references and appendices. Back to text

(4) Richard Pyle, The importance of Deep Safety Stops, DeepTech Issue 5. A number of web sites too. Practical, Pyle-esque writing. Back to text.

(5) R.D. Vann and E.D. Thalmann in The Physiology and Medicine of Diving. 4th edition, P. Bennett and D. Elliot, Eds. (1993). The encyclopedia. Back to text.

(6) E. B. Maiken, Bubble Decompression Strategies, taped proceedings of tek95 conference, aquaCORPS journal (1995). This may be tough to get. It used to be available from aquaCorps. Back to text.

 

Notes

  • Part II of Bubble Decompression Strategies, representing another one-third of the tek95 talk, was never published. But then, I never wrote it either.... The plan was to address the issues brought up at the end of Part I and show some real world deco schedules calculated using the VPM. Examples VPM schedules can be found in the Santa Barbara Alps article and on the VPMtrimix page.
  • The captions to Figs. 2 and 3 in the DeepTech article (and probably in the manuscript I sent them) were interchanged.
  • The Beer, Balloons, and References subsections were omitted in the DeepTech Article.

 

Acknowledgements

DeepTech article thanks to:

  • Curt Bowen and the late Win Remley. 

 

Credits for photos used to illustrate the DeepTech article should be given to:

  • Steve Zimmerman for the Lake Tahoe, NV photo.
  • Steve Maiken for the Pilot Island, Death's Door, WI photo.  

 Back to top